Wormhole Culverts Part 1
Introducing the “Wormhole Method” for including long culverts in a 2D HEC-RAS model
- Wormhole Culverts Part 1: Introducing the wormhole concept
- Wormhole Culverts Part 2: Using wormhole culverts for internal boundary conditions
- Wormhole Culverts Part 3: Comparing wormhole culverts to 1D/2D bridges and culverts
- Wormhole Culverts Part 4: Sensitivity analyses for wormhole culverts
- Wormhole Culverts Part 5: What’s the best shape for a wormhole culvert?
May 2018 update
[PLEASE NOTE: Wormhole culverts have become obsolete with the release of HEC-RAS Version 5.0.4. See our new article on what’s new in 5.0.4 for instructions and videos on using the new culvert options.]
An 18 July 2016 post on the RAS Solution forum by user ckatsoulas provides a workaround for entering culverts into a 2D HEC-RAS model with the inlet and outlet located some distance apart.
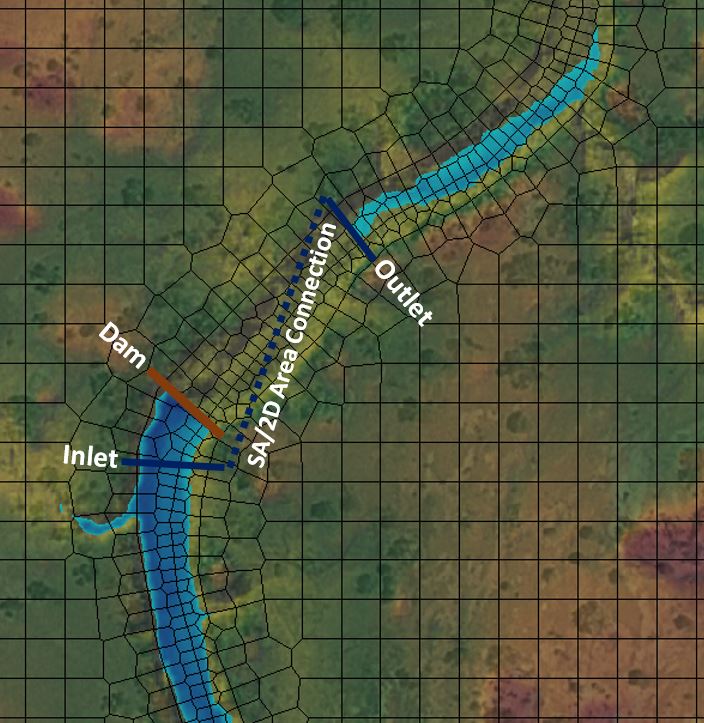
This method basically uses a ground-level weir with culverts as an SA/2D Area Connection, with the inlet and outlet separated along the embankment stationing. I have applied the method on a number of models and can confirm that it works. Here’s a screenshot of the schematic setup of one of my test runs with the resulting water depths:
I’ve decided to call this the “Wormhole Method” since it can essentially transport flow instantaneously between weir/embankment stations, regardless of how far apart they actually lie…perhaps a little something like this:
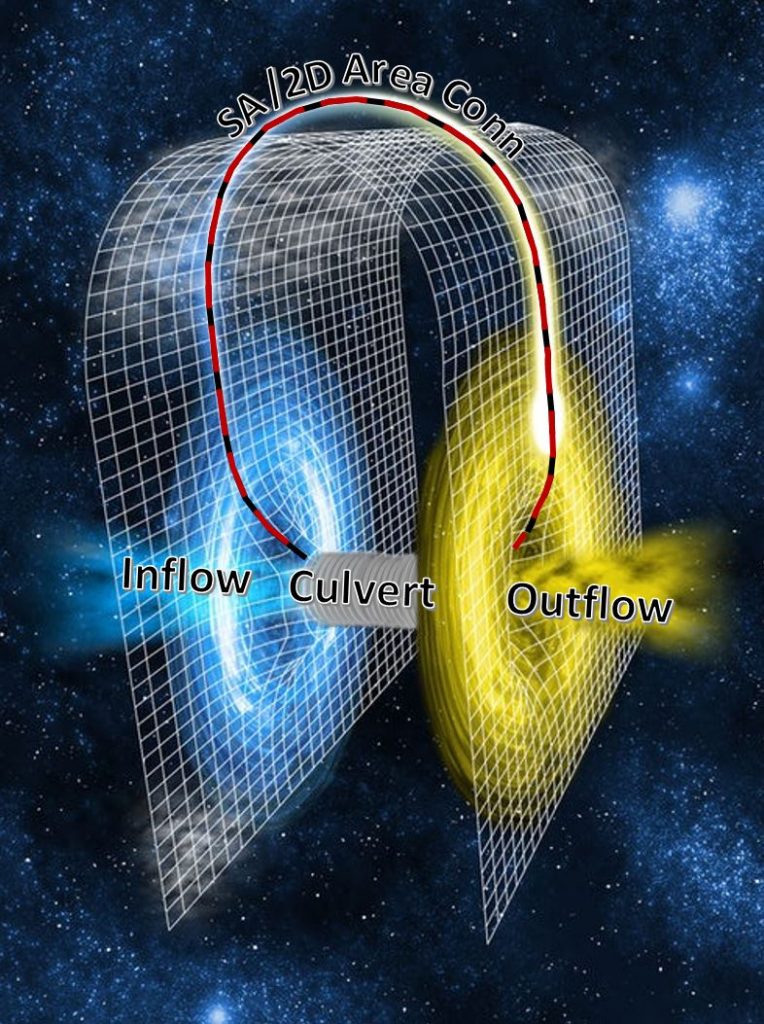
Background image © space.com
This technique has always been do-able in 1D models but I had not tried it yet in a full 2D model, so I thought I’d give it a shot. Here is the link to the original forum post:
http://hec-ras-help.1091112.n5.nabble.com/long-culverts-tp2856.html
The post states:
“I have found a way to create long culverts between two points a distance away and wanted your feedback on the suitability of this method. I basically draw a weir connection with a culvert in a z-shape. The head of the ‘z’ is placed on the upstream point and the tail of the ‘z’ is then dragged anywhere around the 2D area. The trick is to position the inlet at a station that lies at the head of the ‘z’ and the outlet is skewed so that it sits at a station on the tail of the ‘z’. I then check the existing terrain along the weir object and copy and paste the levels to the weir level table. I then enter the culvert details and when I run the job the water goes into the inlet and spills out at the tail of the z-shape. I can extend the weir object anywhere on the map and as long as I keep my weir at the ground level I don’t disturb the natural runoff and can even do rain on grid model runs.”
This method provides a workaround for one of the current limitations of HEC-RAS acknowledged in the February 2016 HEC-RAS 2D manual (Page 6-64), which states:
“Note: Currently the Internal Hydraulic structures are limited to connecting cells along faces. Hydraulic outlets such as gates and culverts can only be connected from the cells on one side of the structure to the cells on the other side of the structure. In future versions we will allow culverts, gates, etc. to be connected to cells upstream and downstream of the structure that are some distance away from the structure (i.e., you will be able to specify the X and Y coordinates of the culvert of gate entrance and exit).”
Some of my mine site models have floodways (low-level, dip, or ford crossings) for separate LV and HV traffic lanes where the inlet and outlet of the culverts that cross below the floodway are upwards of 80 metres apart. Forcing these models to connect adjacent cells (with terrain elevations that have to be lower than the culvert invert) in this instance is completely impractical, requiring the incorporation of a 1D reach into the model or complete removal of the roadway embankment in the terrain. The Wormhole Method allows the road crossings to be modelled completely as 2D terrain with the inlet and outlet on opposite sides of the floodway.
I have also used this method as a workaround to add an internal boundary condition for inflows, which is covered in Part 2 of this series of articles.
Before we get too far ahead of ourselves, however, to really understand where wormhole culverts come from we have to first go back to a 1D structure in HEC-RAS.
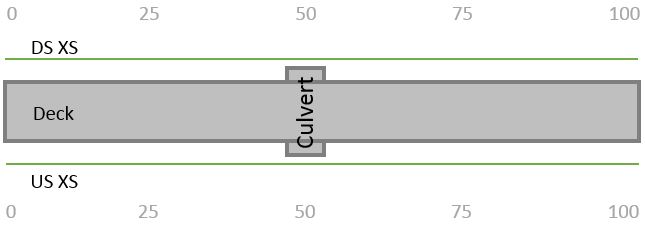
A 1D model with a bridge/culvert requires bounding cross sections along the channel adjacent to the upstream and downstream bridge face. In the schematic example below, in which the bounding cross sections start at the same station and cover the same distance parallel to the bridge deck, both the upstream and downstream centerline stationing for the culvert would be identical; in this case, you would enter “50” for each value:
If the cross section stationing differs between the upstream and downstream bounding sections, however, the culvert centerline values can be adjusted accordingly. In the case below, for example, the upstream centerline station would be entered as “50” and the downstream station would be “25”:
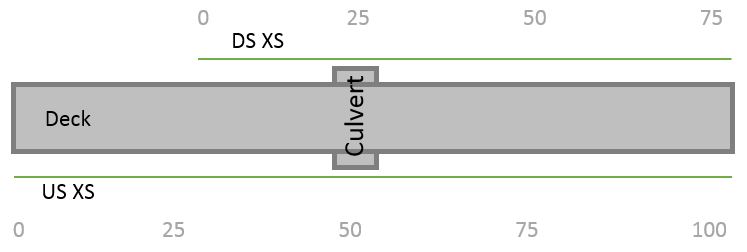
The 25 meter difference in stationing does not affect the culvert hydraulics; only the length of the culvert itself figures into the balance. The stationing of the cross section is rather arbitrary, and we could just as well assign the starting station to be 1,000 rather than 0 for any of the cross sections in the above examples without any impact whatsoever on the hydraulics. The intention of allowing different stations for the upstream and downstream culvert centerline in a 1D model is not to move the culvert but to represent the actual, fixed location of the culvert against the arbitrary, adjustable cross section stationing – allowing flow to be kept in the correct portion of the channel. If you entered culvert centerline station values that ended up moving flow to another channel or branch in a 1D model, it would probably be the result of an unintentional coding error.
As we move into 2D, however, everything is georeferenced, and any difference between the upstream and downstream culvert centerline station values represents an actual shift in the flow path along the alignment. Because the current limitation of HEC-RAS is to connect culverts to the grid cells immediately adjacent to the connection line, using standard methods there would generally be no reason for the upstream and downstream culvert centerline station values to differ significantly. Using the concept of wormhole culverts, however, the difference in the numerical value of the station represents a deliberate shift in the inlet and outlet locations. I’ll illustrate that concept with the simplest of cases, in which we have a culvert that is oriented perpendicularly to a roadway alignment:

By differing the upstream and downstream culvert centerline stationing, we are still drawing from the hydraulic properties of the cells that touch the connection line, but we are essentially breaking the culvert in half and shifting the outlet to another location along the roadway alignment:
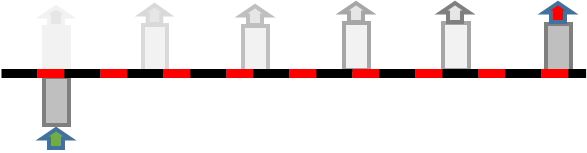
For a standard culvert, this wouldn’t be a realistic scenario. In the case of a wormhole culvert, however, instead of following an actual roadway alignment with our connection line, we are creating an imaginary, at-grade roadway that can wind its way anywhere throughout the model without affecting the two-dimensional flow in the surrounding computational mesh. Discharge through the culvert is still one-dimensional in nature; the hydraulic computations for a wormhole culvert use the assigned culvert length, inlet/outlet configuration, roughness, slope, and other properties to balance the headwater and tailwater levels at the grid cells immediately adjacent to the inlet and outlet stationing, but these two cells can now be located anywhere in your model. They do not need to be adjacent, and the distance between the inlet and outlet in the schematic view (measured along the connection line) is ignored entirely in the computations.
I’ll include an example below where I’ve used the Wormhole Method to simulate outlet works on a dam. Here is a creek system that is modelled as a 2D Area:
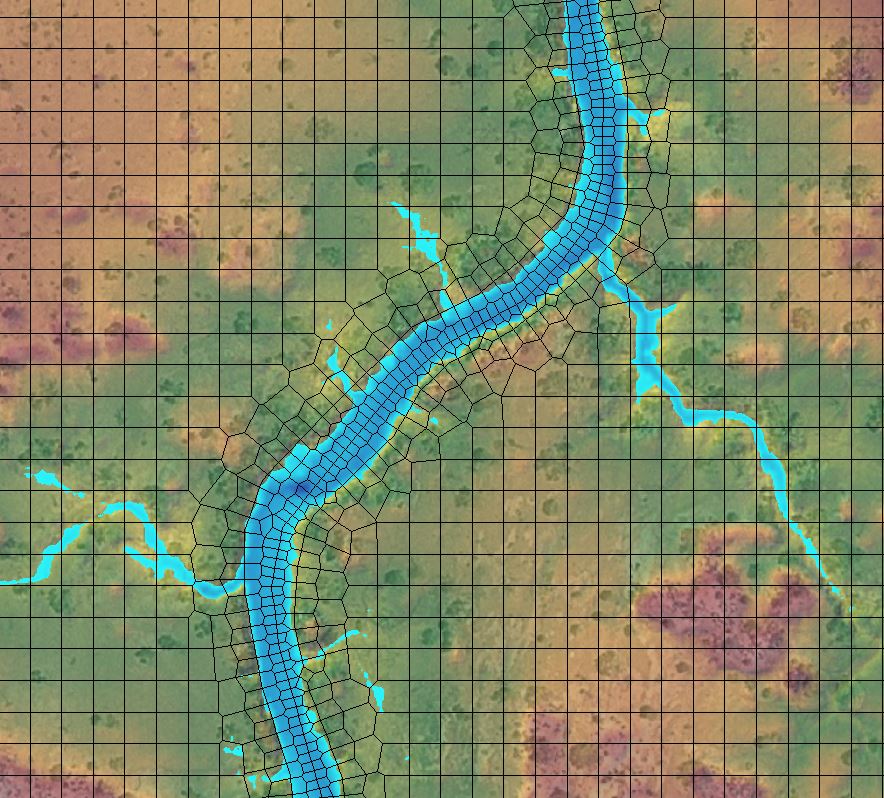
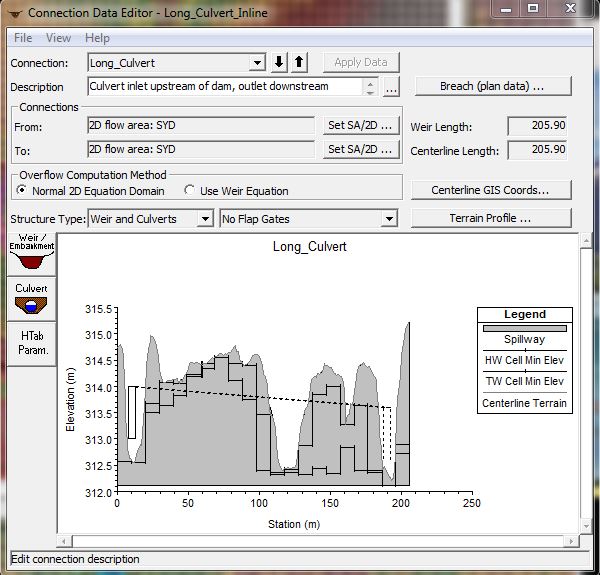
I use the “SA/2D Area Conn” button along the Tools ribbon to add a dam across the creek and set the Weir/Embankment crest elevation above the channel banks.
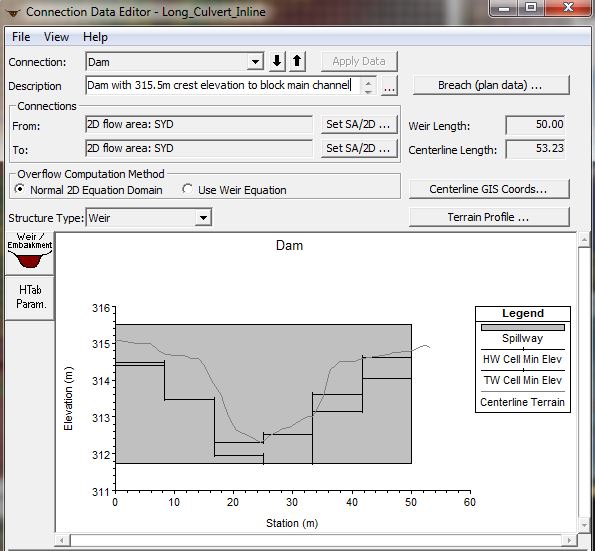
Here is the dam profile (entered using the “SA/2D Area Conn” button along the Editors ribbon).
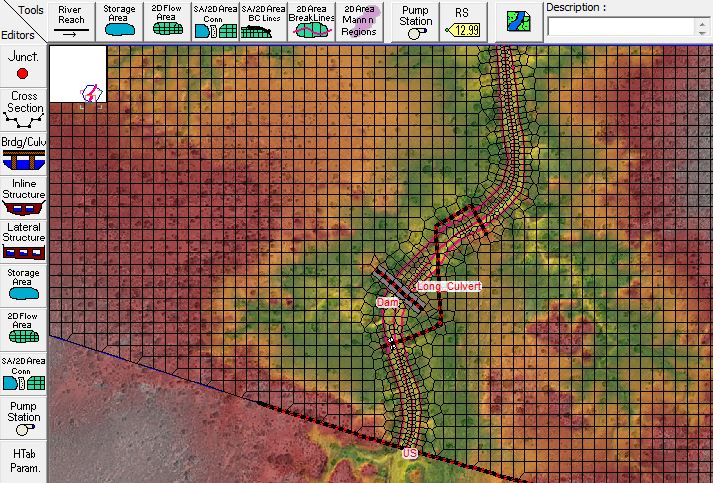
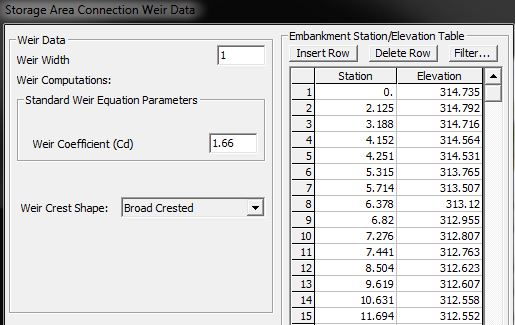
I then add a second SA/2D Area Connection to simulate the culvert inlet and outlet locations. I orient the line left to right looking downstream across the channel upstream of the dam, then cross the channel and change directions again to keep the flow orientation pointed downstream at the outlet. (The optimal shape for a wormhole culvert is covered in Part 5). The alignment will snap to the cell faces but can be smoothed by enforcing the internal connection as a breakline (though that’s not required unless your grid size is very large relative to the length of the alignment). I then use the “Terrain Profile” button and copy/paste the profile data to the Weir/Embankment editor. This introduces a weir along the selected alignment that matches the existing terrain and therefore does not affect the hydraulics. Essentially it’s just a line painted on the ground. Keep in mind that you will need to set the overflow computation method to “use normal 2D equation domain” rather than the weir equation as described in more detail here.
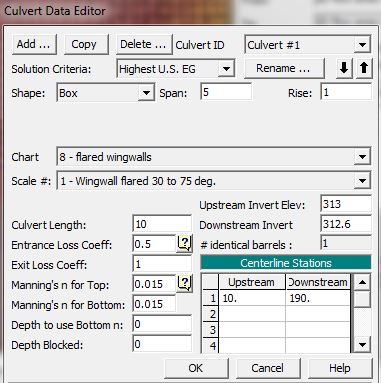
I then add a culvert with the inlet in the first (upstream) main channel. I skip the second (middle) main channel crossing and add the outlet at the third (downstream) creek crossing, ensuring that the culvert invert is above the ground elevation in the terrain surface. The schematic plan view representation of the culvert will be incorrect (it will be centered on the connection line at the upstream station and oriented perpendicular to the line). But the locations shown for the inlet and outlet in plan view are not used in the 2D analysis anyway (since the current version of HEC-RAS can only draw flow in or discharge flow out to the grids located immediately adjacent to the connection line, regardless of where the schematic shows them).
When I rerun the model with the structure in place, flow backs up behind the dam, and when it reaches the invert elevation of the upstream culvert, flow begins to appear at the downstream outlet location, skipping the mesh cells in between. Here’s how it appears in RAS Mapper:

This particular scenario could represent an outlet pipe that has been tunneled through the dam embankment with discharge re-entering the channel at the downstream outlet location. I can adjust the culvert length, width, height, diameter, etc. to change the arrival time or the flow rate through the culvert and – with enough iterations – match any hydrograph I wish to introduce.
Instead of using a short ‘z’ shape, we can also use a long, snaking ‘s’ shape to move the inflow to an adjacent tributary, as shown in Part 2 of this series of articles.
The Wormhole Method works best when the bridge deck or roadway crest elevations are included in the terrain data, with the ‘z’ alignment crossing the bridge deck as shown in the examples in Part 3. As with the other bridge workarounds in 2D models, any results generated by this method would greatly benefit from calibration against a localized 1D model or actual observations. None of these workarounds should be used to design an actual structure, and all of the other disclaimers that are stated in this blog post about bridges in 2D areas would apply to the wormhole culvert workaround as well. But if the focus is on flood levels or other elements that are affected by the presence of a long culvert or bridge without requiring the actual design details for the structures themselves, this method of instantly teleporting the flow along embankment stations seems to function quite well.

The original forum post didn’t generate any responses, but to me it appears to be an ingenious workaround (that hopefully won’t be required anymore when Version 5.1 is released). This method has always worked in 1D models, but I would appreciate further input on its validity for 2D situations. So far I have mainly used it to force a desired amount of inflow into a system by adjusting arbitrary culvert dimensions without testing whether the system would reasonably be able to provide that inflow over the assigned distances. I have done some limited sensitivity testing (see Part 3) on a very simple model, but I would be very interested in any additional testing results that other users might be able to provide in order to determine whether the culvert hydraulics are in fact reasonable. In the meantime, given some of the current limitations of HEC-RAS, the Wormhole Method is just what I’ve been looking for – thanks Con!
Read more:
- Wormhole Culverts Part 1: Introducing the wormhole concept
- Wormhole Culverts Part 2: Using wormhole culverts for internal boundary conditions
- Wormhole Culverts Part 3: Comparing wormhole culverts to 1D/2D bridges and culverts
- Wormhole Culverts Part 4: Sensitivity analyses for wormhole culverts
- Wormhole Culverts Part 5: What’s the best shape for a wormhole culvert?
Contact and feedback:
- Please e-mail me any comments or questions about wormhole culverts or other topics
- Contribute to the discussion about wormhole culverts on the RAS Solution blog
- Subscribe to receive updates when new content is published
- Join the newly created LinkedIn groups for dam break modelling and sediment transport modeling
Krey Price
Surface Water Solutions
